Extended Certainty Factors utilizing Neutrosophic Logic
Main Article Content
Abstract
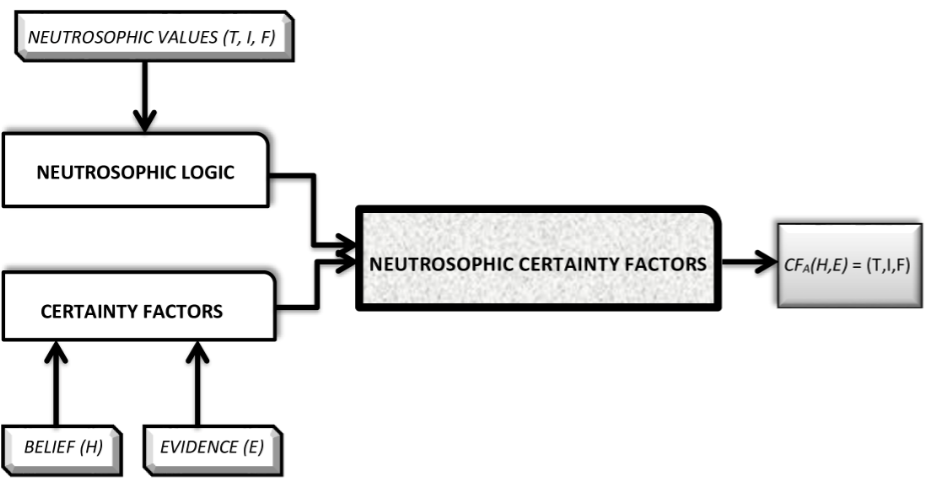
Addressing uncertainty is a significant challenge in the field of artificial intelligence (AI). AI systems often encounter uncertainty due to incomplete data, ambiguous information, or inherent unpredictability in specific situations. To tackle this uncertainty, various solutions have been developed. These solutions range from probabilistic approaches like Bayesian networks and Monte Carlo methods to fuzzy logic and neural networks. These strategies enable AI systems to model and make judgments amid ambiguity by assigning probabilities, dealing with imprecise data, or utilizing learning processes that adapt to changing and uncertain contexts. However, probabilistic methods have limitations when it comes to handling uncertainty. These limitations include assumptions of independence, computational complexity, difficulty in capturing subjectivity, and interpretability. To address these limitations, other methods have been proposed, such as the model of certainty factors. This model offers a framework for reasoning under uncertainty by assigning a numerical value to statements or propositions. Additionally, neutrosophic logic extends classical logic by incorporating the concept of indeterminacy through truth/indeterminacy/falsity-membership functions. In this paper, we propose a method for investigating how certainty factors adapt to a neutrosophic environment. This method contributes to the development of more robust and adaptable decision support systems capable of dealing with diverse uncertainty. Our method, introduced for the first time in related literature, addresses issues such as the limited handling of indeterminacy, the inability to address contradictions, and the limited binary representation of uncertainty that characterize the model of certainty factors. We will provide a clear illustration of these implications through an example that demonstrates the superiority of our suggested method over the traditional technique of certainty factors.
Downloads
Article Details

This work is licensed under a Creative Commons Attribution 4.0 International License.