Permutation Graphs in Fuzzy and Neutrosophic Graphs

Abstract

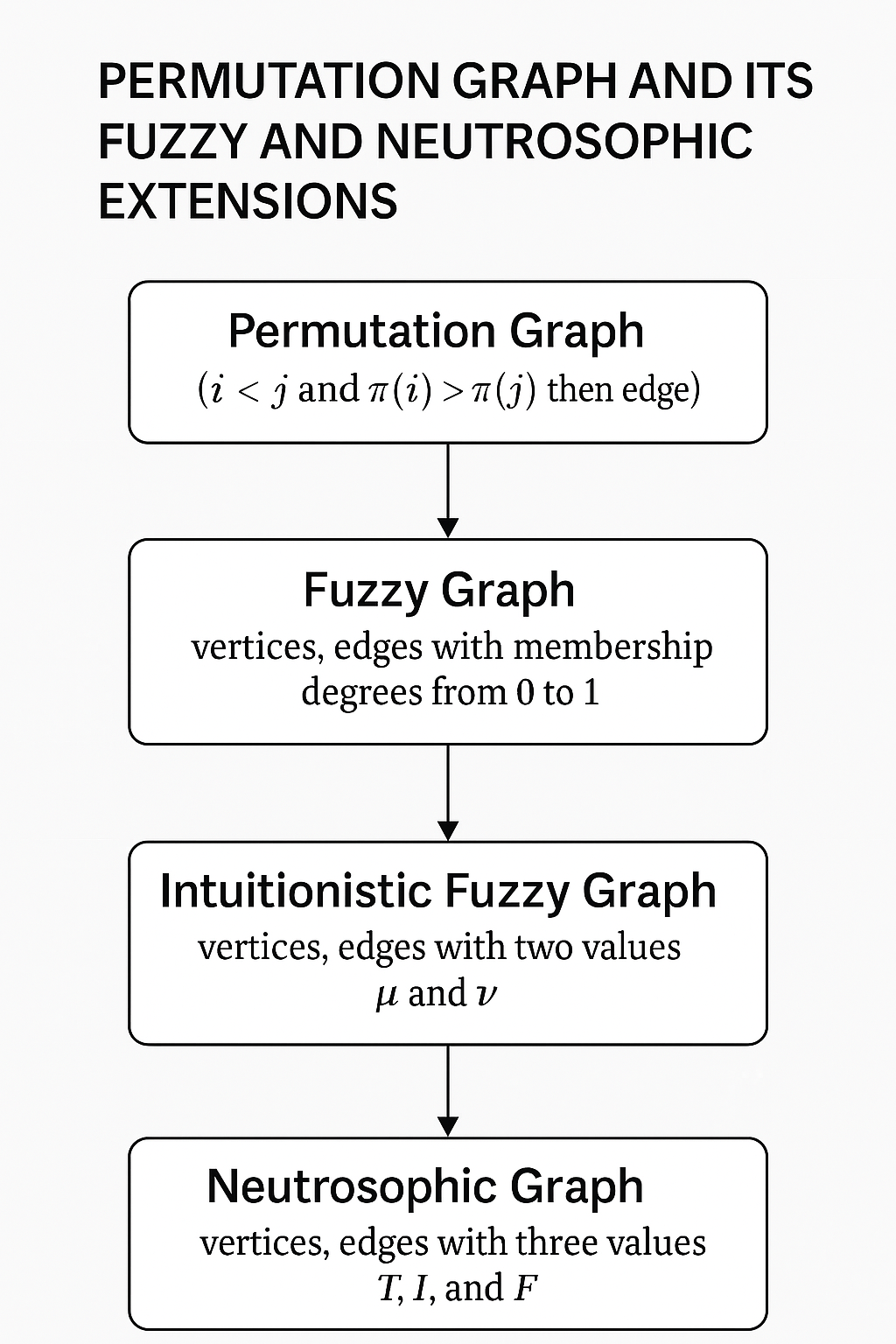
Graph theory is a fundamental branch of mathematics that examines networks composed of nodes (vertices) and connections (edges). This paper explores the concepts of permutation graphs within the frameworks of fuzzy, intuitionistic fuzzy, neutrosophic, and Turiyam Neutrosophic graphs, all of which handle uncertainty in graph structures. We define permutation and bipartite permutation graphs in each context and investigate their properties. While permutation graphs have been studied extensively in classical graph theory, there has been limited exploration in fuzzy and neutrosophic settings.