3-Dimensional Quartic Bézier Curve Approximation Model by Using Neutrosophic Approach

Abstract

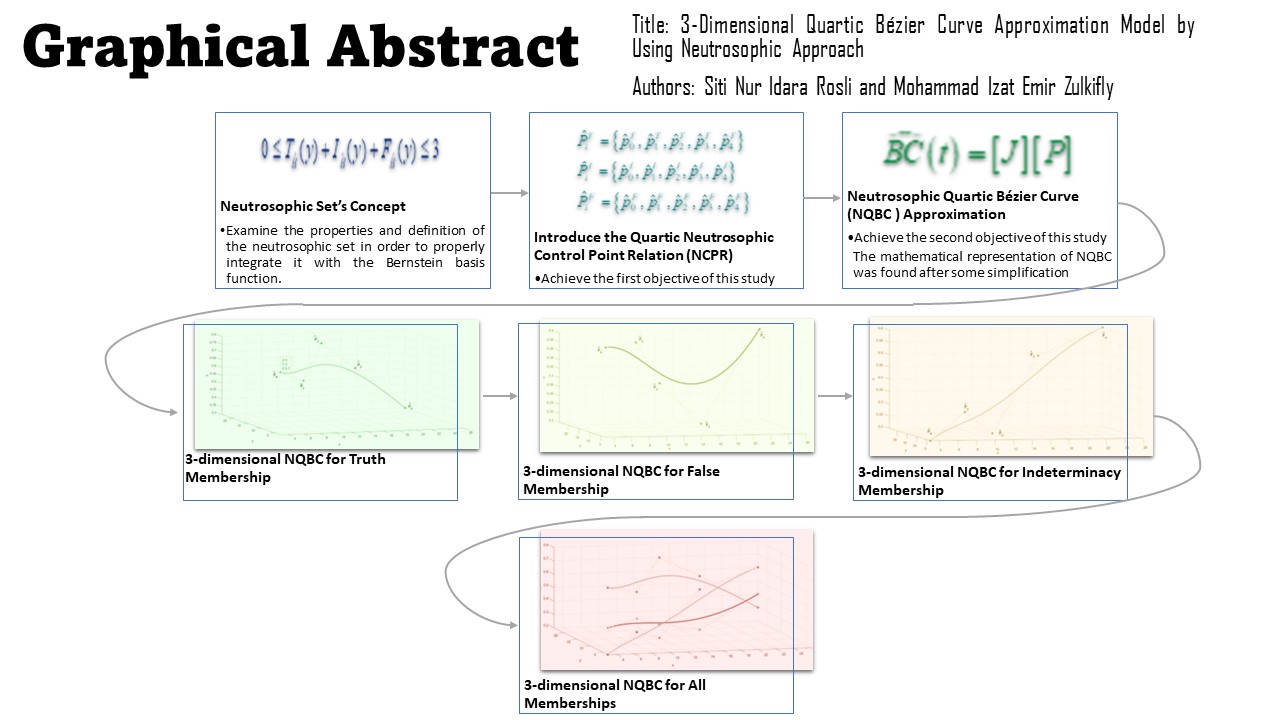
In a 3-dimensional data collection process, there exists noise data that cannot be included to visualize the process. Therefore, it is difficult to deal with since fuzzy set and intuitionistic fuzzy set theories did not consider the indeterminacy problem. However, using a neutrosophic approach with three memberships: truth, false, and indeterminacy membership function, the error data will be treated as uncertain data by using the indeterminacy degree. Thus, this study will visualize the 3-dimensional quartic Bézier curve model by using neutrosophic set theory. To construct the model, the neutrosophic quartic control point must first be introduced to approximate the neutrosophic quartic Bézier curve. Next, the Bernstein basis function as the methodology of this study will be blended with the neutrosophic fundamental notion. At the end of this paper, a numerical example of the 3-dimensional neutrosophic quartic Bézier curve will be visualized by using the approximation method as the finding of this study. Finally, this study provides significant contributions to making it easier for data collectors to visualize all data, which means that no data will be eliminated since the uncertainty data will also be used.