A Study on the Polarity of Generalized Neutrosophic Ideals in BCK-Algebra

Abstract

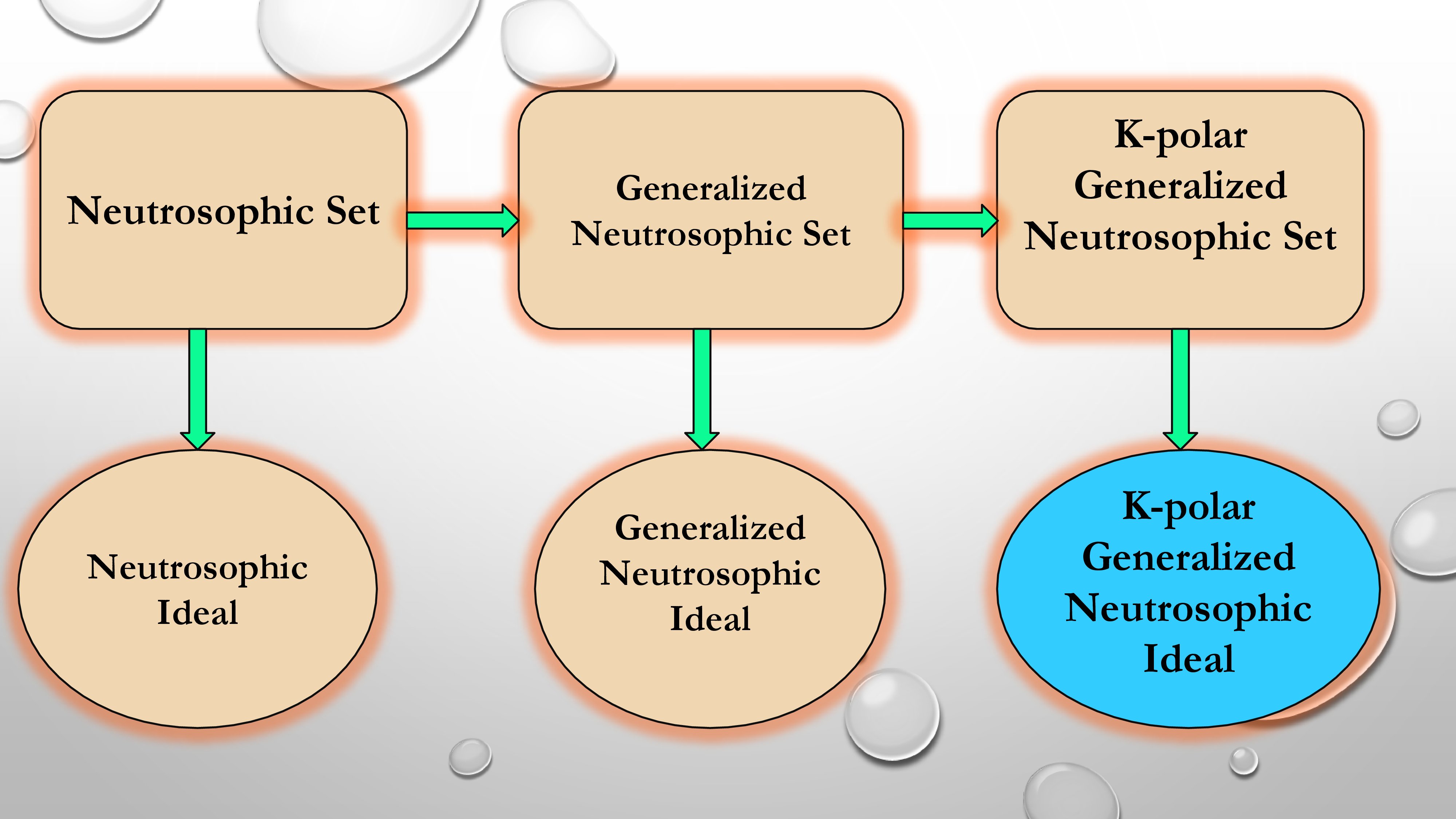
In this study, we apply k-polar generalized neutrosophic logic to the ideal of BCK-algebra and consequently introduce the notion of a k-polar generalized neutrosophic ideal in BCK-algebra with an example. We provide conditions for a k-polar generalized neutrosophic set to be a k-polar generalized neutrosophic ideal. We prove that every k-polar generalized neutrosophic ideal is a k-polar generalized neutrosophic subalgebra, but the converse is not true, which can be illustrated with an example. Furthermore, we prove that a k-polar generalized neutrosophic set is a k-polar generalized neutrosophic ideal if and only if its corresponding cut sets are ideals of the BCK algebra.