Maxwell’s Equations Optimizer (MEO): A New Physics based Metaheuristic Optimization Algorithm for Solving Optimization Problems

Abstract

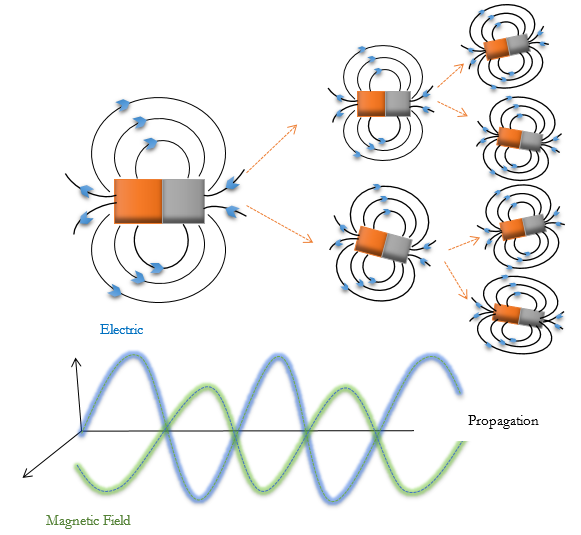
In this paper, a new metaheuristic algorithm inspired by the principles of physics called Maxwell's Equations Optimizer (MEO) is presented. Maxwell's are considered one of the most well-known equations in the field of physics. These equations are a set of four equations that describe the behavior of electric and magnetic fields, their interactions and the influence of objects. Simulating how equations behave is the core concept of MEO. These equations behave according to two main behaviors. They are as follows:  divergence behavior, and curl behavior. Divergence measures the tendency of the charge to collect or disperse at a point (exploration phase), while curl measures the tendency of the charge to swirl around the point (exploitation phase). By tracking these two behaviors, Maxwell was able to reach the electromagnetic wave by introducing the idea that the electric field and the magnetic field are two sides of the same coin. Accordingly, this behavior was simulated and the proposed algorithm was presented. Two phases of exploration and exploitation are used to explain and mathematically model the MEO implementation processes. By choosing the best charge, which has the best ability to diverge in space and create the best electromagnetic field around it, the MEO optimizer finds a balance between exploration and exploitation. The effectiveness of the suggested algorithm (MEO) is assessed using the 24 unimodal standard functions varies (fixed and variable dimension) and 44 multimodal standard functions varies (fixed and variable dimension). The source code is publicly accessible at https://drive.mathworks.com/maxwell.